數據結構(平衡二叉數)
數據結構(平衡二叉數)
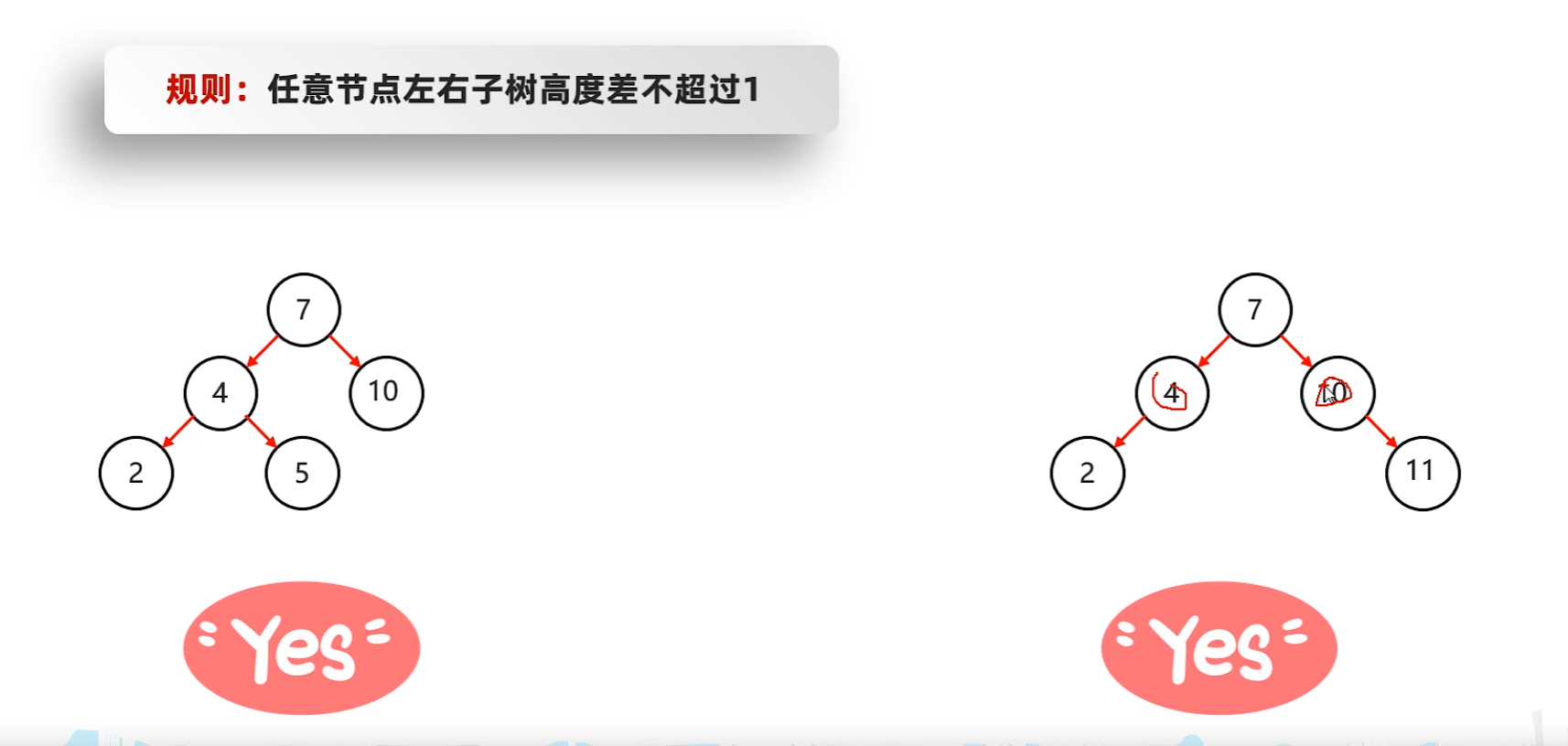
-
怎樣的機制可以保證高度差呢?
- 旋轉機制
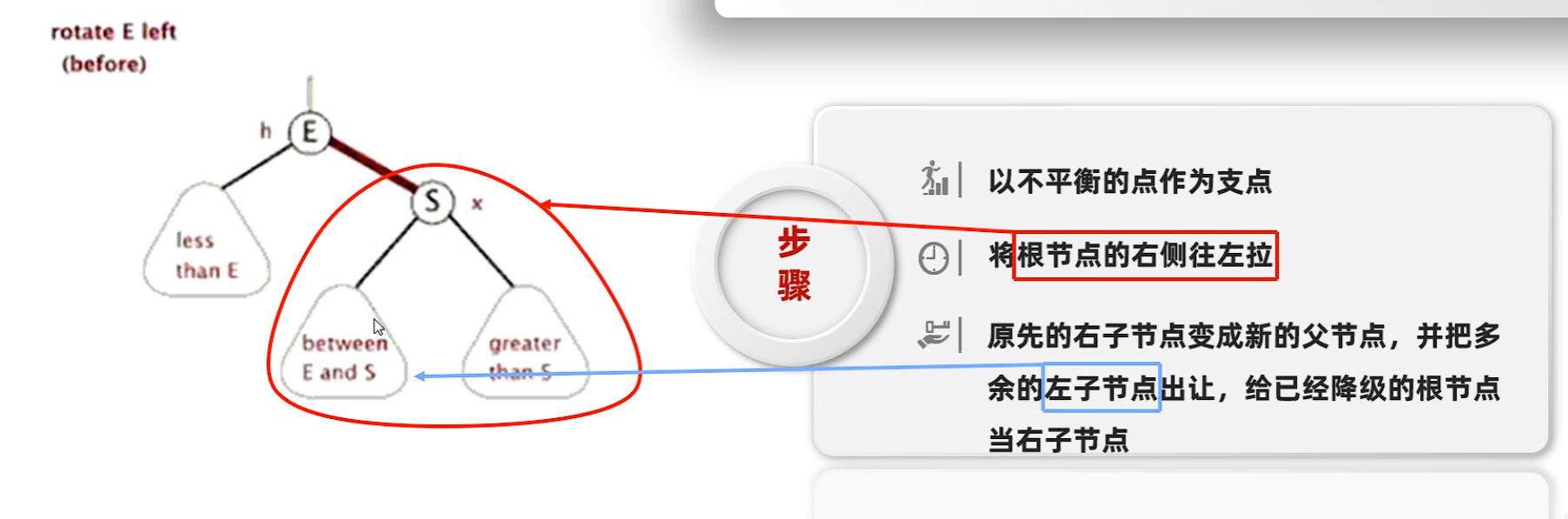
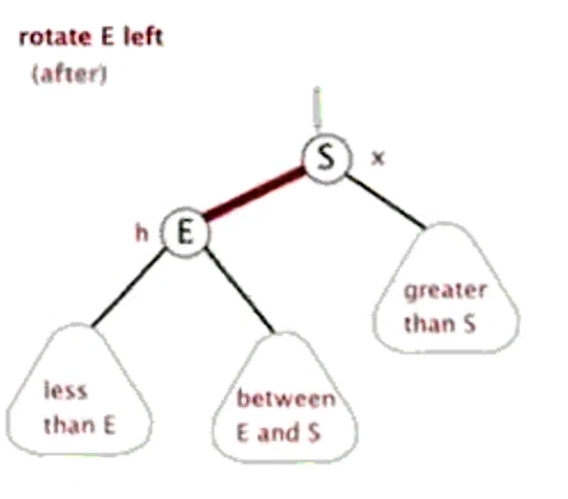
- 左旋
- 右旋
- 觸發時機:當添加節點後,該樹不是平衡二叉樹了
- 旋轉機制
-
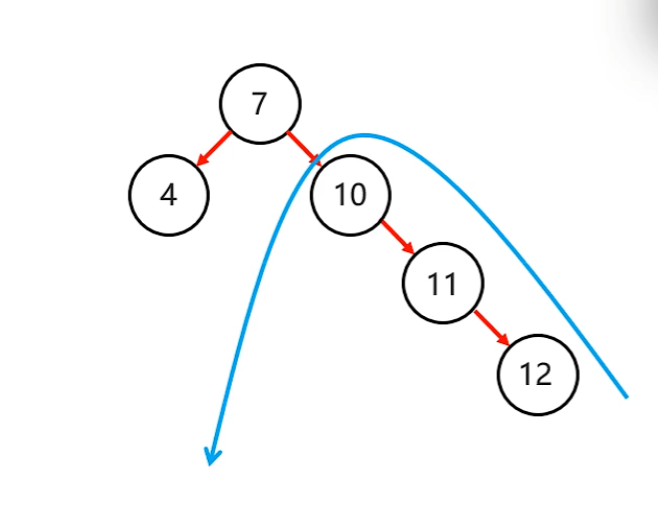
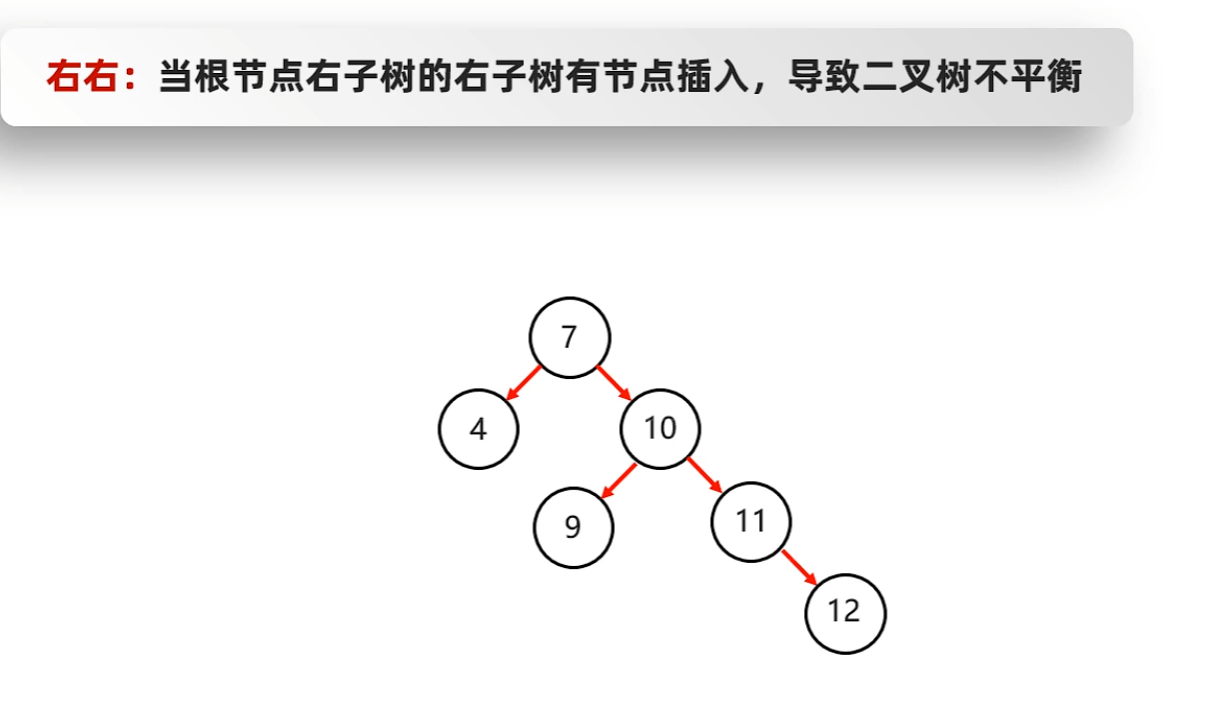
左旋
- 確定支點:
- 從添加的節點開始,不斷往父節點找不平衡的節點
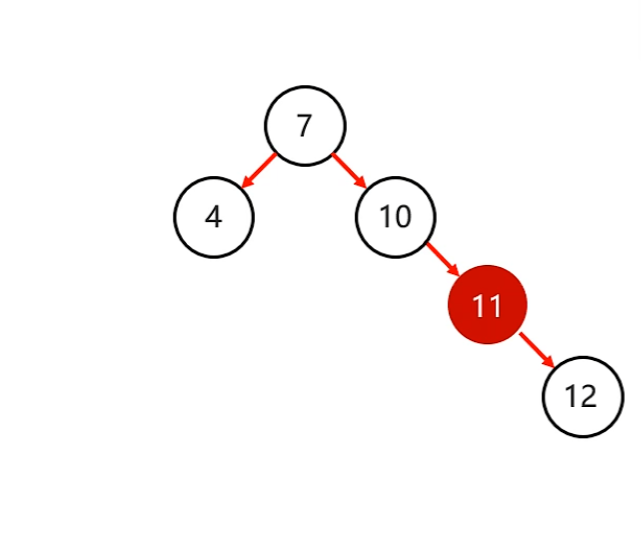
- 一路找到10節點
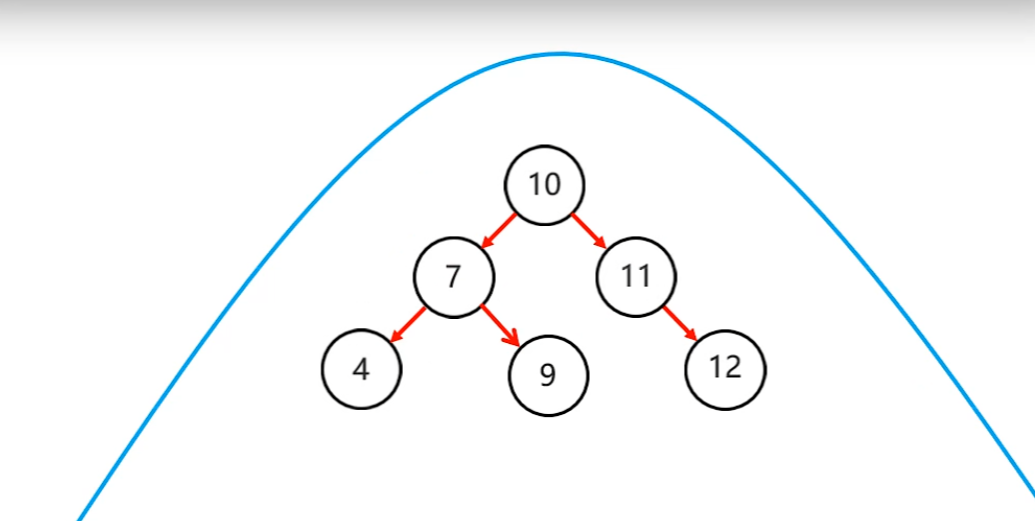
- 旋轉步驟

- 10節點當左子節點
- 11當父節點
- 12當11的右子節點
- 在根節點呢?
- 確定支點:
-
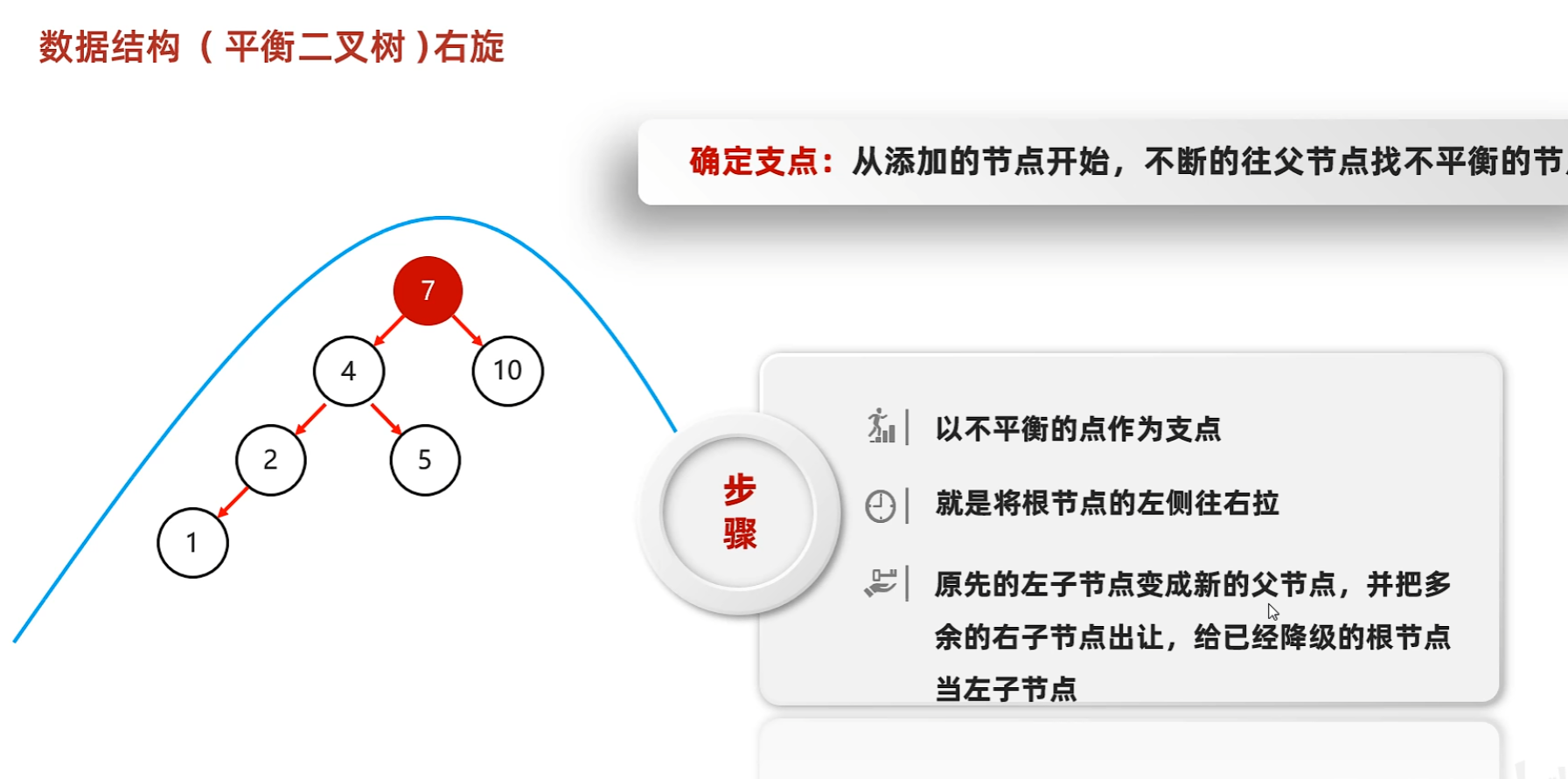
右旋
- 確定支點:
- 從添加的節點開始,不斷往父節點找不平衡的節點
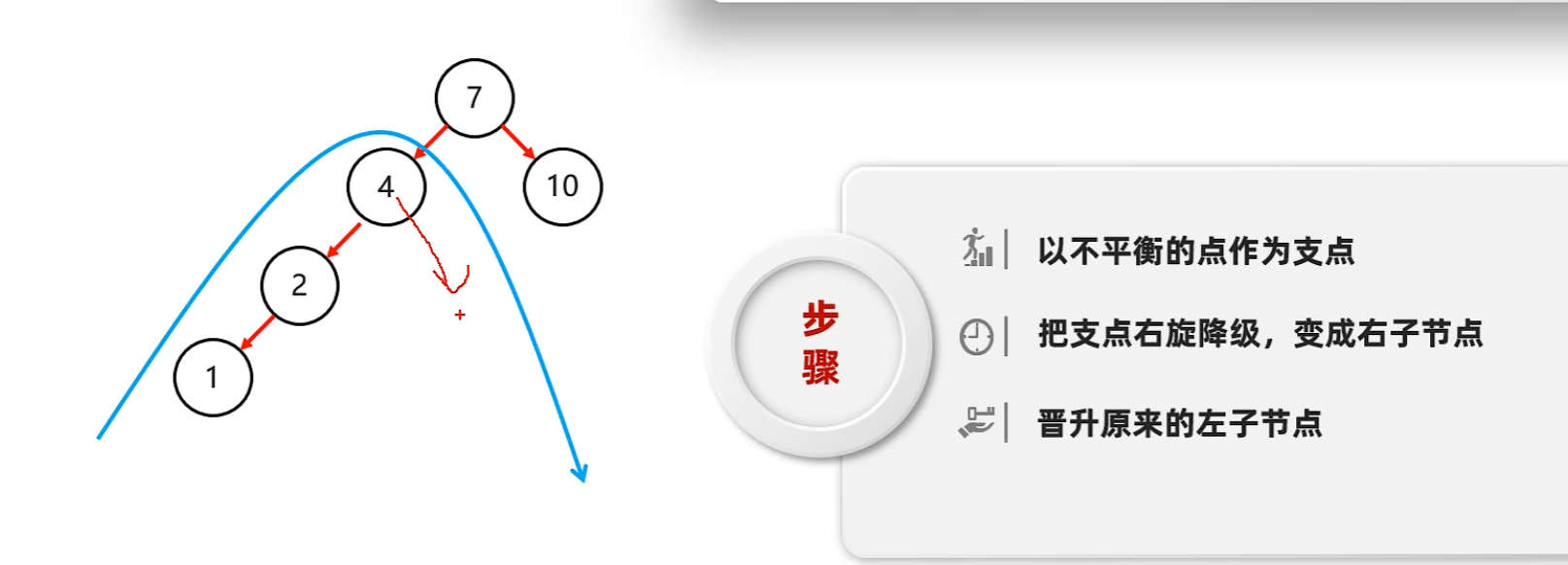
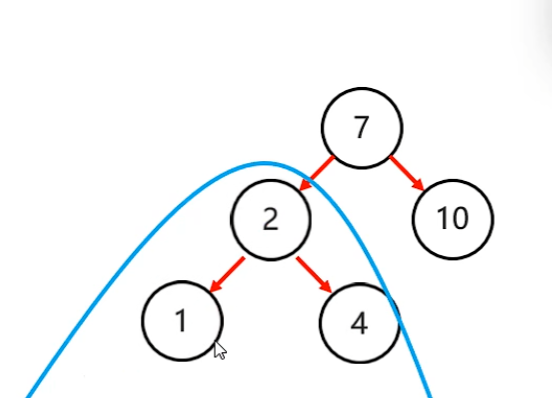
- 在根節點呢?
- 確定支點:
-
需要旋轉的四種情況
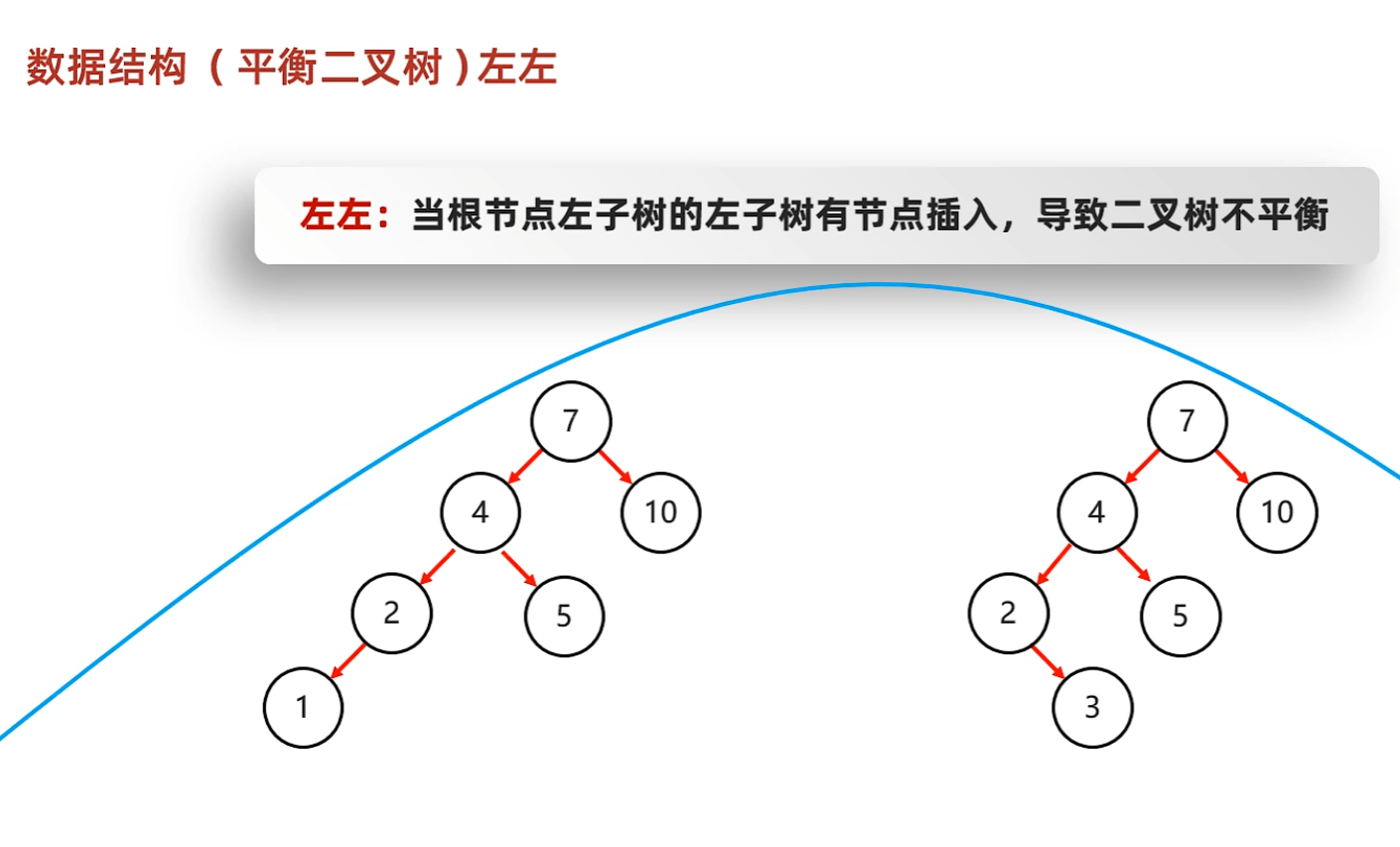
- 左左 --> 一次右旋
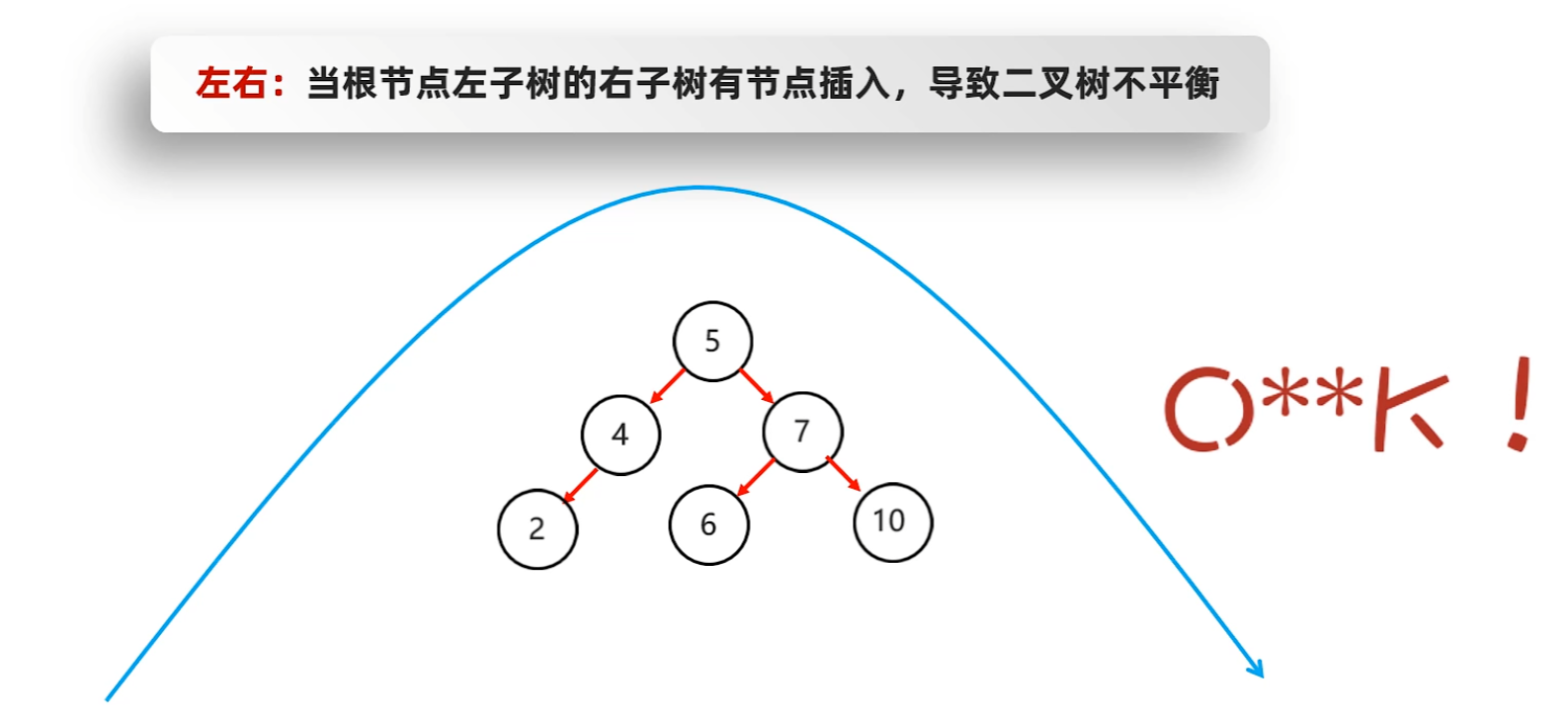
- 左右 --> 先局部左旋再整體右旋
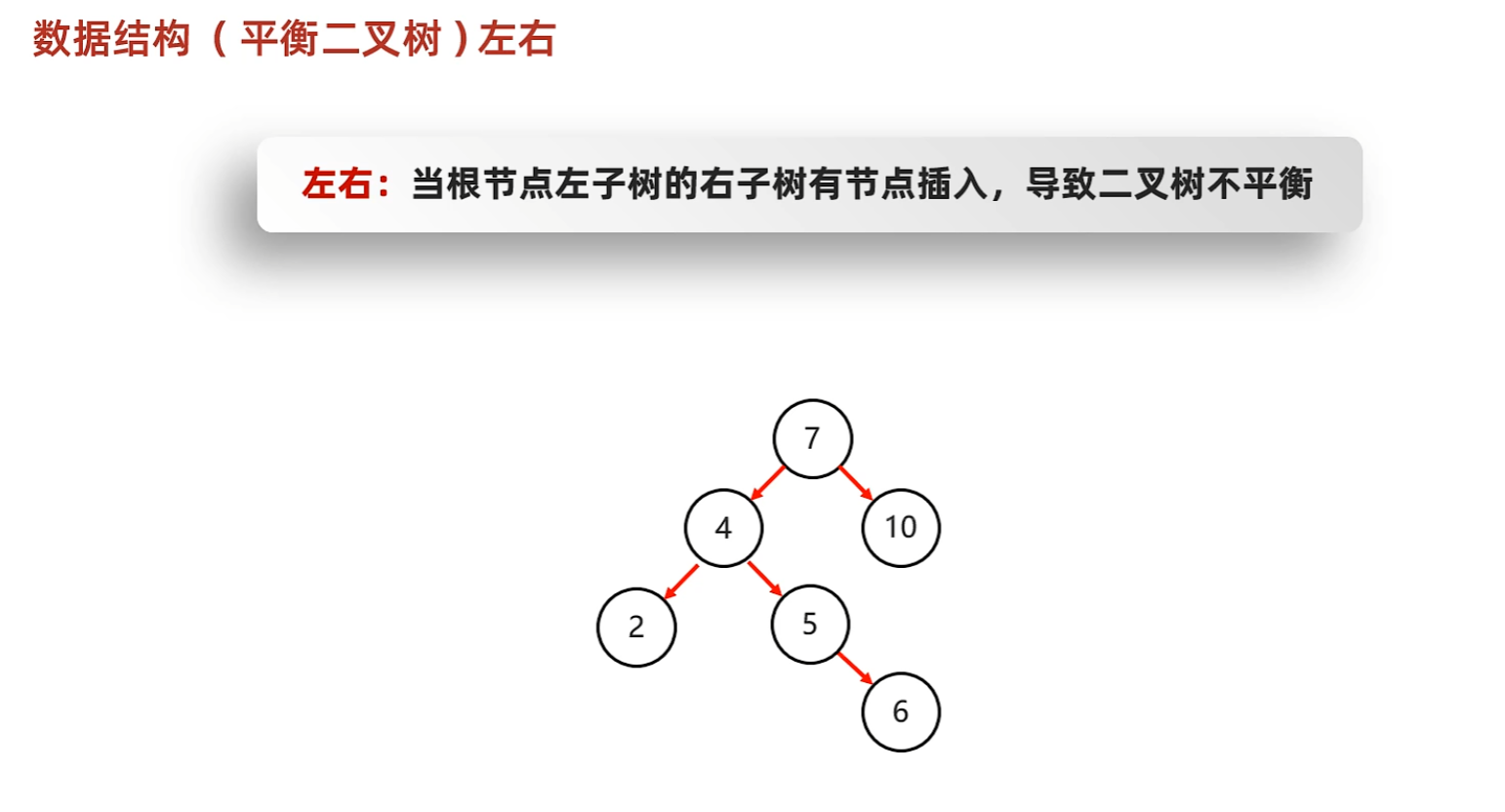
- 先局部左旋
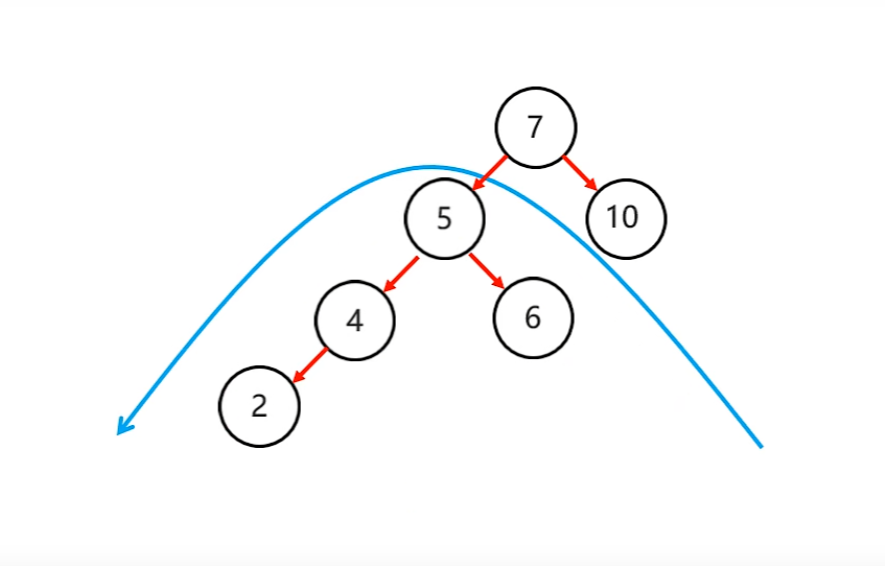
- 在整體右旋
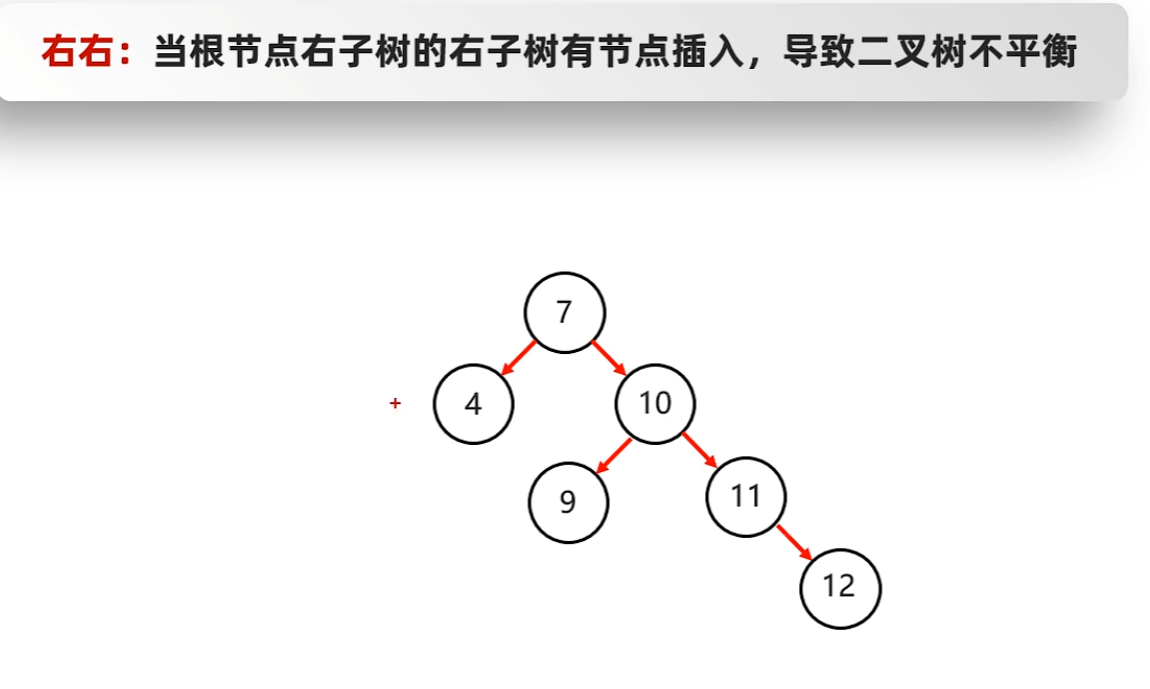
- 右右 --> 一次左旋
- 右左 --> 先局部右旋再整體左旋
- 先局部右旋
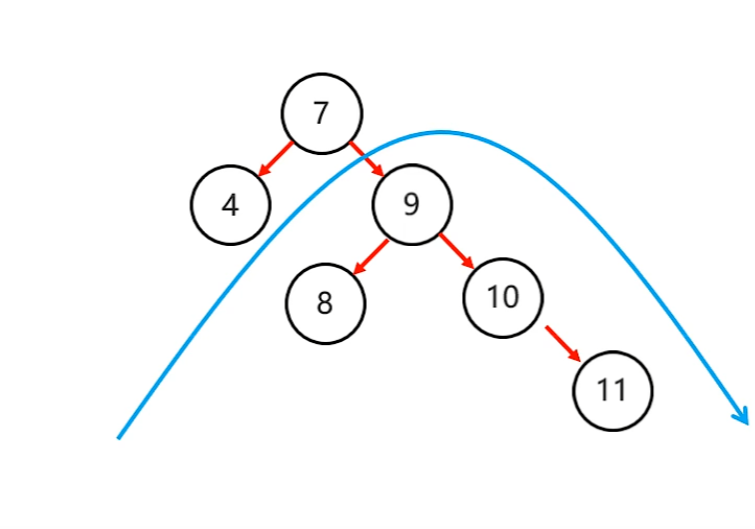
- 再整體左旋
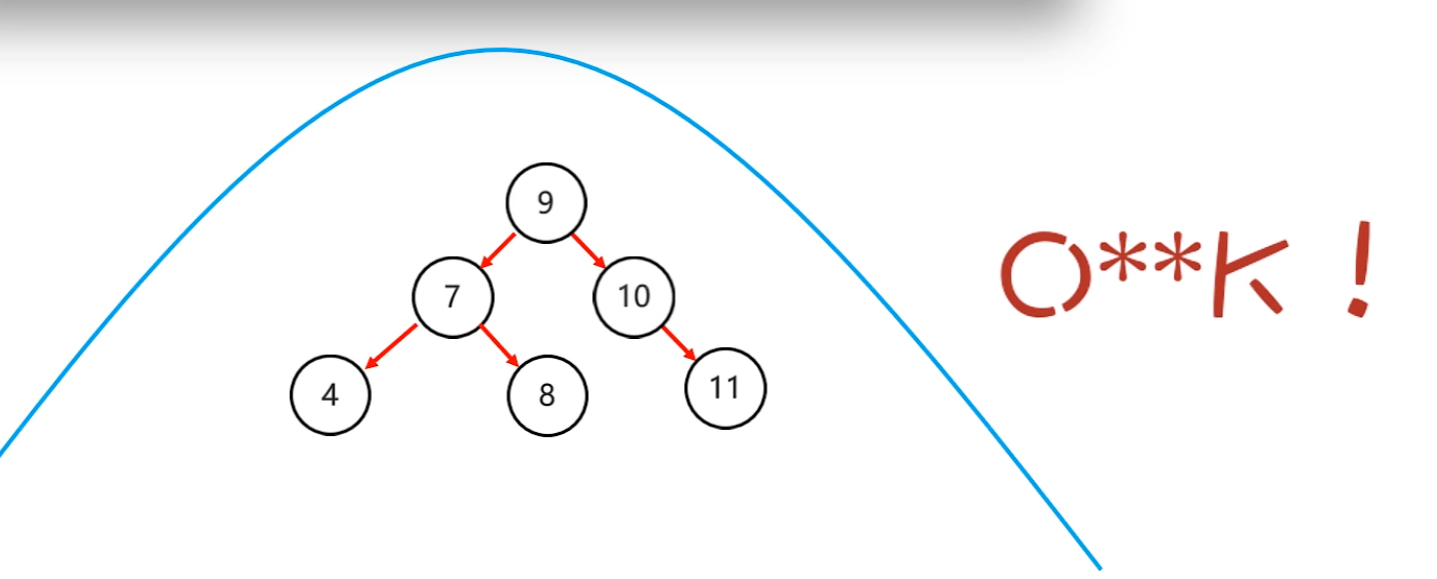
- 左左 --> 一次右旋
小結
- 普通二叉數 --> 查詢效率差 --> 出現二叉搜索數(查詢效率高)
- 二叉搜索數 --> 會機率出現長短腿 (會變成單向鍊表)--> 出現平衡二叉樹
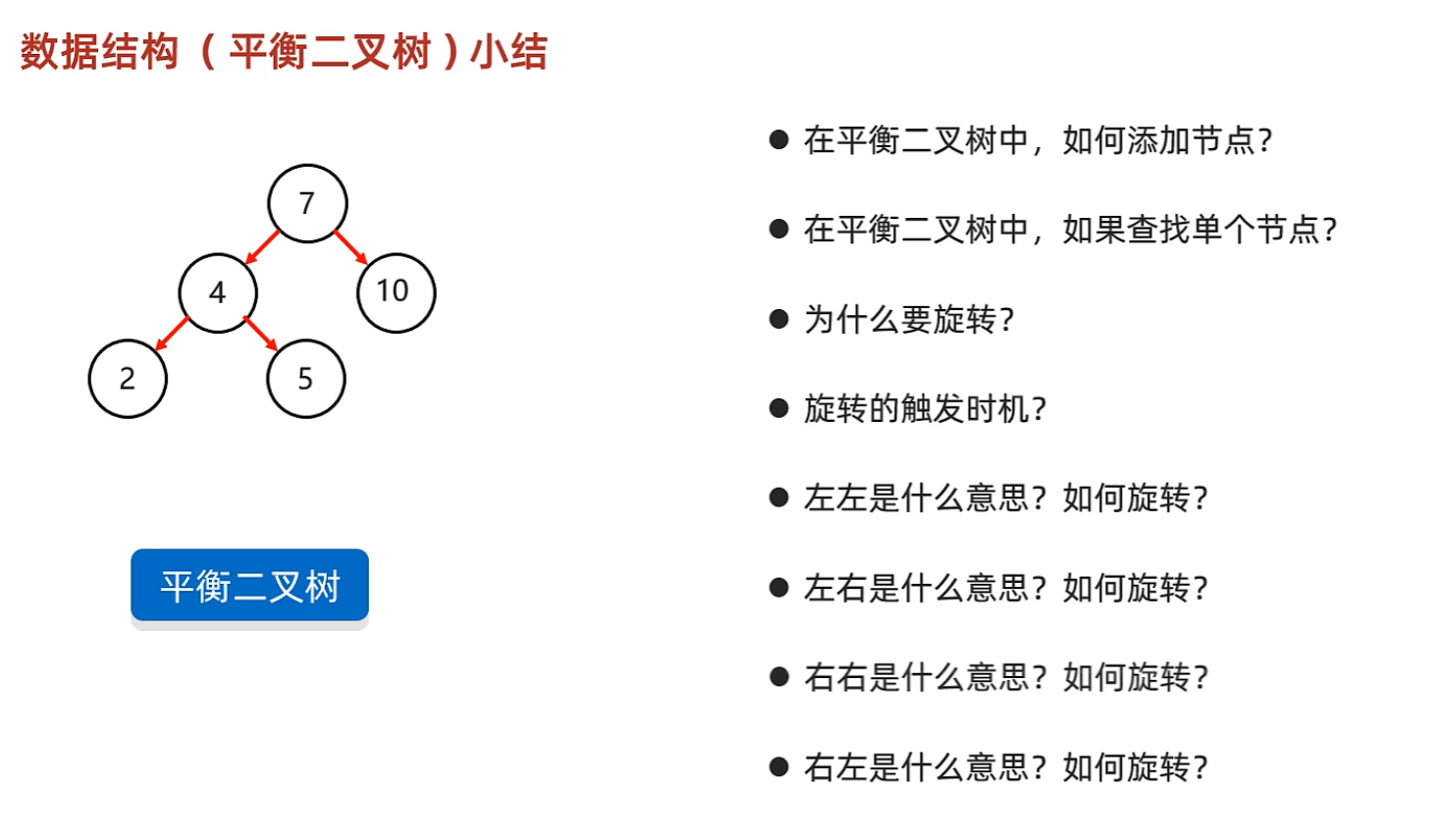
- 1.新增節點:小的在左,大的在右,重複的不要
- 2.如果目標比節點大 --> 往右找,反之往左找
- 3.為了要平衡整個數的節點,透過旋轉平衡二叉數
- 4.如果添加節點後,破壞該樹的平衡
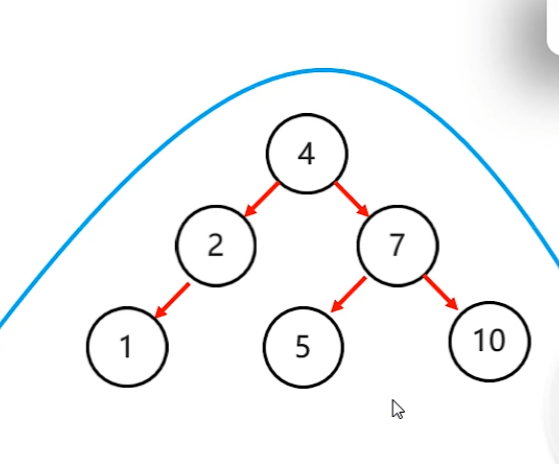
- 5.新的節點在根節點左邊子樹的左邊子樹上,左左 --> 一次右旋
- 6.左右 --> 先局部左旋再整體右旋
- 7.右右 --> 一次左旋
- 8.右左 --> 先局部右旋再整體左旋